

In these systems, certain sets of directions are symmetrically equivalent to each other. Many crystal systems have elements of symmetry. The difference between lattice directions and lattice vectors is that a lattice vector has a magnitude which can be shown by prefixing the lattice vector with a constant. The direction in which the lattice vector is pointing is the lattice direction. Lattice directions are written the same way as lattice vectors, in the form. This lattice vector would be written in the form: One of the first steps in modeling a solid material is to determine the lattice parameters for the material. Instead a bar is placed above the number to denote that the value is negative: Negative values are not prefixed with a minus sign. In shorthand, lattice vectors are written in the form: Any lattice vectorĬan be written as a linear combination of the unit cell vectors a, b, and c: Their number can be smaller in the case of symmetries in the unit cell for example, there is only one spatial lattice parameter in a cubic cell, a. There are six lattices parameters, three dimensions, and three angles. (often also called ‘unit cell parameters’, or just ‘cell parameters’).Ī lattice vector is a vector joining any two lattice points. The lattice parameters are quantities that indicate the shape of a crystalline cell. Γ are collectively known as the lattice parameters However, for an SCC lattice a step change was seen in the energy vs lattice parameter plot. There are several ways to describe a lattice. The smallest group of symmetrically aligned atoms which can be repeated in an array to make up the entire crystal is called a unit cell. The angles between the crystallographic axes are defined by: For a fair comparison of the crystal energies, using a constant cut-off energy of 775 eV and a 12x12x12 grid in the reciprocal space, lattice parameters were varied for BCC, FCC and SCC lattices. Bravais Lattice refers to the 14 different 3-dimensional configurations into which atoms can be arranged in crystals.
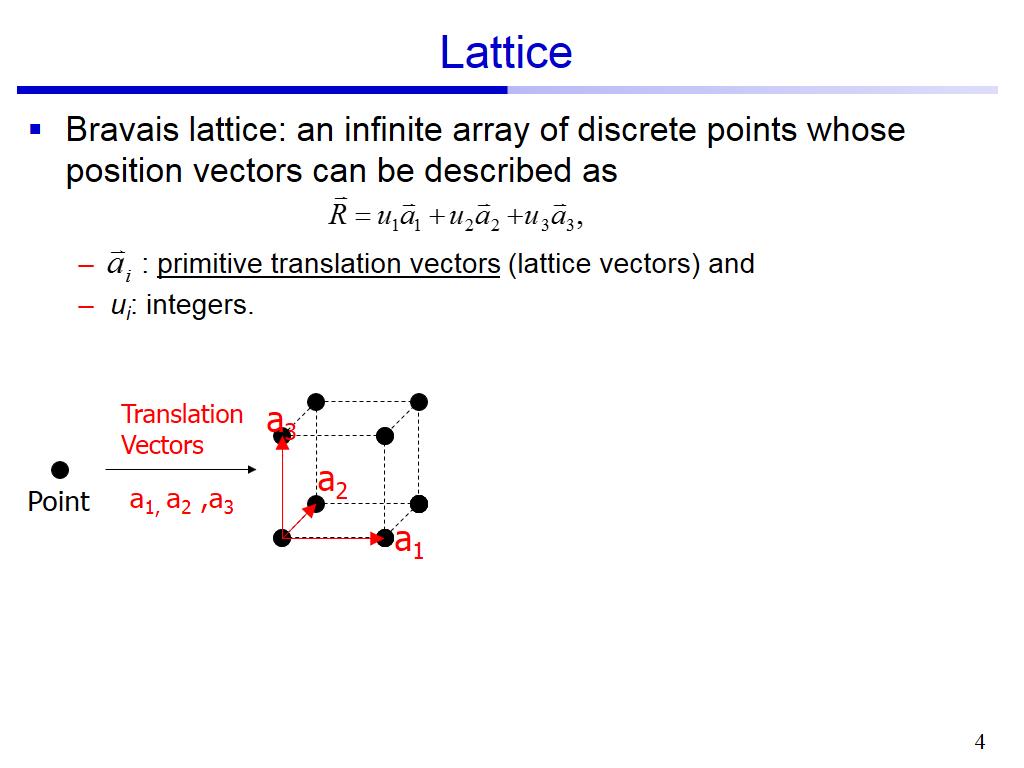
The sides of the unit cell in terms of vectors a, The length of the unit cell along the x, y, and The origin of our coordinate system is at one of the lattice points. Set of crystallographic axes, x, y, and z, which point along the edges of the To define the geometry of the unit cell in 3 dimensions we choose a right-handed In this video, Parisa works through the calculation of the lattice parameter for the face centered cubic (FCC, or cubic close packed) crystal structure, in terms of the atomic radius.


 0 kommentar(er)
0 kommentar(er)
